Selected Publications
Pulse reshaping effects that give rise to fast and slow light phenomena are inextricably linked to the dynamics of energy exchange between the pulse and the propagation medium. Energy that is dissipated from the pulse can no longer participate in this exchange process, but previous methods of calculating real-time dissipation are not valid for extended propagation media. We present a method for calculating real-time dissipation that is valid for electromagnetic pulse propagation in extended media. This method allows one to divide the energy stored in an extended medium into the portion that can be later transmitted out of the medium, and that portion which must be lost to either dissipation or reflection.
The idea of a book being a collection of pages is so ingrained that modern electronic book readers often try to faithfully reproduce this feature--up to elaborate simulations of page turns. However, traditional pages are not necessary and often inconvenient in electronic books. It is often easier to scroll the text than to turn the pages, and text reflowing makes the use of folios a rather strange way to refer to the position inside a text. We argue that it is more natural to paginate electronic books according to their logical structure, when a \page" corresponds to a sectional unit of the book. This leads to rather long pages, with the height of the page depending on the length of the corresponding unit. We discuss how to implement these pages in TEX and provide a basic introduction to output routines in TEX for a beginning TEXnician. We also provide exercises for a slightly more advanced reader.
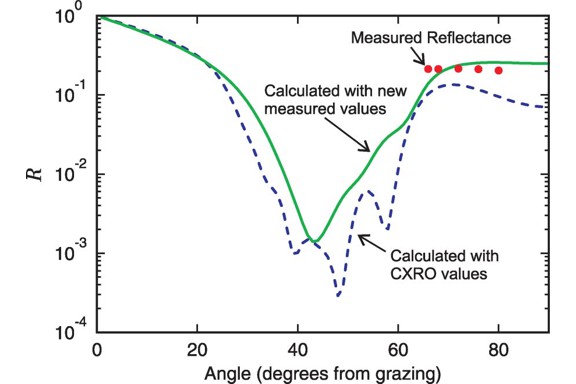
We use a laser high-harmonics-based extreme-ultraviolet (EUV) polarimeter to determine the optical constants of elemental uranium in the wavelength range from 10 to 47 nm. The constants are extracted from the measured ratio of p-polarized to s-polarized reflectance from a thin uranium film deposited in situ. The film thickness is inferred from a spectroscopic ellipsometry measurement of the sample after complete oxidation in room air. Uranium has been used as a high-reflectance material in the EUV. However, difficulties with oxidation prevented its careful characterization previous to this study. We find that measured optical constants for uranium vary significantly from previous estimates. (C) 2010 Optical Society of America