Selected Publications

Michael J. Ware (et al.)
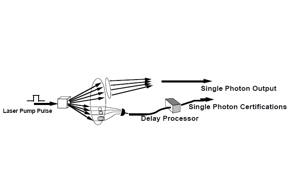
We present the status of our work implementing a single photon on-demand source based on a multiplexed arrangement of parametric downconverters. An array of downconverters with multiplexed outputs makes it possible to create light pulses with increased probability of containing a single photon, while suppressing the probability of producing more than one photon. This is crucial for quantum cryptographic applications. Our current setup implements the scheme in a greatly simplified manner that produces photons along with a measure of the likelihood that the light pulse emitted is just a single photon. This implementation uses a virtual array of downconverters and an array of staggered length optical fibers allowing a single detector to measure a herald photon output by a series of downconverters. This single detector arrangement is a great savings considering the cost of such detectors. The timing of the herald tells us which path the herald took, which in turn, provides information on the single vs. multiphoton probabilities. So far, our work shows that the individual correlated photon peaks are clearly resolvable with our 2.4 ns delay line steps and the 1 ns full width half maximum (FWHM) of the correlated photon peaks, and that we can observe four correlated photon peaks simultaneously, a requirement to fully implement our scheme. Our current efforts are to increase the brightness and utility of the system for incorporation into a quantum communication testbed.
M. Ware, S. Glasgow, and J. Peatross