Selected Publications
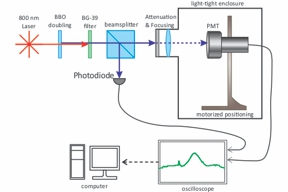

We present calibrated measurements of single-photon Thomson scattering from free electrons driven by a laser with intensity 1018 W/cm2. The measurements demonstrate that individual electrons radiate with the strength of point emitters, even when their wave packets spread to the scale of the driving-laser wavelength. The result agrees with predictions of quantum electrodynamics.
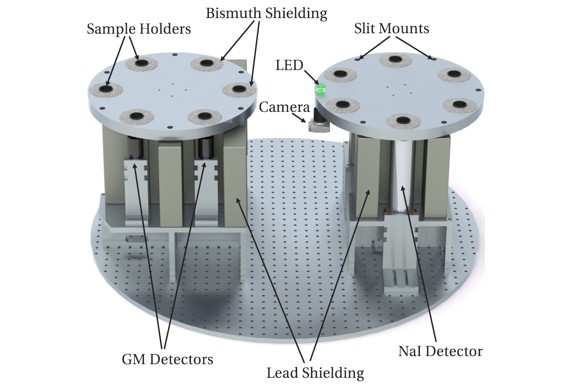
We describe an experimental setup for making precision measurements of relative β-decay rates of Na-22, Cl-36, Mn-54, Co-60, Sr-90, Ba-133, Cs-137, Eu-152, and Eu-154. The radioactive samples are mounted in two automated sample changers that sequentially position the samples with high spatial precision in front of sets of detectors. The set of detectors for one sample changer consists of four Geiger-Müller (GM) tubes and the other set of detectors consists of two NaI scintillators. The statistical uncertainty in the count rate is few times 0.01% per day for the GM detectors and about 0.01% per hour on the NaI detectors. The sample changers, detectors, and associated electronics are housed in a sealed chamber held at constant absolute pressure, humidity, and temperature to isolate the experiment from environmental variations. The apparatus is designed to accumulate statistics over many years in a regulated environment to test recent claims of small annual variations in the decay rates. We demonstrate that absent this environmental regulation, uncontrolled natural atmospheric pressure variations at our location would imprint an annual signal of 0.1% on the Geiger-Müller count rate. However, neither natural pressure variations nor plausible indoor room temperature variations cause a discernible influence on our NaI scintillator detector count rate.